主题:向各位高人求救一道离散数学的证明题:急用!谢谢! -- 锦候
Theme: Pascal -Fibonacci
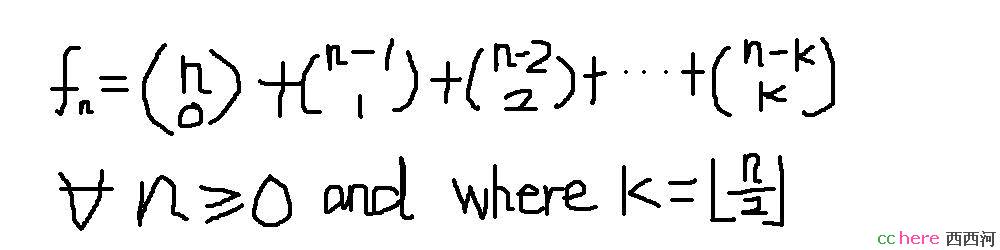
这里的k 是一个floor 方程, 这个题要证明fibonacci number可以用这种方式表达。要求是不能用induction来证明。
实在是想不出来了,周2考试要考,各位数学高手大侠帮帮忙!谢谢了!
本帖一共被 1 帖 引用 (帖内工具实现)
思路:
你可以考虑一下K为什么会那样取值?
提示:
在n元集合中不包含相邻元素的子集最多能有几个元素?
n>1 只要证明 Fn+1=Fn+Fn-1
奇数偶数分开证,
用Pascal's rule (n,k)=(n-1,k-1)+(n-1,k)
只剩下第一项,不过它反正都是1.
don't get it, more details plz!
more is better.
I need more details.thx.
你那个公式的f(n) 处理的是包含n-1个元素集合的所有不相邻元素子集的数目。
第一项也可以写成 (n-1,0).这样,每一项就是就是刚好包含i个不相邻元素子集的数目。i=0到K。
这个也需要证明,但很简单,自己完成吧。
剩下的就是,证明包含n个元素的不相邻元素子集的数目是兔子数列。
只要证明递推公式就可以了。
这也不难,假定任意一个集合A,那么n要么属于A要么不属于
如果不属于,那么集合A必然对n-1的情况有效。
如果属于,那么n-1必然不在其中,此时再从A中拿掉n,则必然对于n-2的情况有效。
于是 f(n)=f(n-1)+f(n-2)
我这个方法好处是比较直观,能理解其中的数学内涵。
Doob兄的方法做起来肯定更快,直接代入公式,计算则可。
n=2k+1
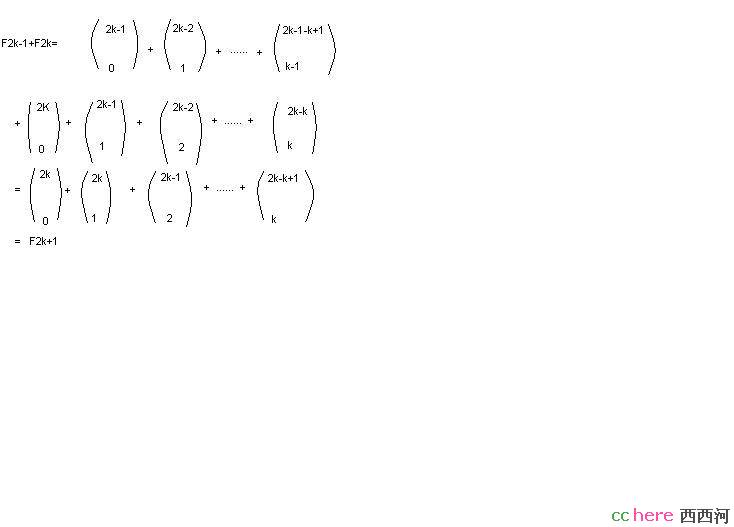
这里用了Pascal's rule (n,k)=(n-1,k-1)+(n-1,k)
第一行各项加第二行对应项等于第三行。
n偶数时,同样可证。
还有哪个k的取值范围,也不明白。
您受累给做一遍行吗?一步步来一下,我有很多地方不明白。这门课确实也是上的吃力。谢谢!
恭喜:你意外获得【通宝】一枚
鲜花已经成功送出。
此次送花为【有效送花赞扬,涨乐善、声望】
k>=1
k是floor方程,所以奇偶分开。
我上面把奇数的情况证了,n=2k的证明类似。你最好自己证一下F(2k-2)+F(2k-1)=F(2k),看看上面的证明中各项应该换成什么。
我有时看不懂书,自己跟着写一下,会有帮助。
我每次问助教都要一步步的来我才看得明白。实在是太笨了。
要是太麻烦了,您就不要管了。谢谢!
这个东西我们课上没讲,老师提了一下说以后再讲,我们也再没用这个fibonnaci 或者pascal只是知道这是个什么东西罢了,结果就说考试要考了。而且不让用归纳法(inductive)证明,
我没怎么上过这种计算机专业的数学课,这个东西难度对我来说是蛮大的。所以麻烦给个比较详细的步骤,不然我看不明白!啊,各位兄弟姐妹非常拜托,拜托!
(n) (n-1) (n-1)
( )=( )+( )
(m) ( m ) (m-1)
这个公式应当是可以直接用的。
证明步骤:
1,分奇数偶数两种情况,如n=2m,则k=m;如果n=2m+1,则k=m;
2, 对于n,n-1,n-2,把等式横着写,右对齐;
3,对于公式的右边,竖着加,就证明了
f(n)=f(n-1)+f(n-2);
4,对于n=0,n=1验证是Fibonacci数
于是得证。