主题:【原创】电力系统漫谈 (一) 引子 -- 乃力
- 共: 💬 188 🌺 449
怎么讲电力系统稳定问题,是个问题。
一种方法是从最简单的系统模型(单机无穷大母线系统)讲起,逐渐过渡到复杂系统。一开始很容易明白,但很多人(包括当年的我)基本就迷失在这个过渡的过程中。另一种方法是从稳定性和控制论的理论开始讲。结果是什么呢?上过线性系统和非线性系统课的人大概都知道,肯定大多数人直接晕了。而且,如果讲控制理论,与其我讲,不如让晨枫兄或者润树兄来讲为好。
在和一个在某电力公司工作的美国小伙儿聊天之后,我得到了些启发。这个小伙儿本科毕业,曾经搞过些交通信号灯控制。现在改做电力系统分析了,包括静态安全和稳定分析。我学了这么多年,也就是略知皮毛。人家是怎么做稳定分析的呢?于是,我们针对他工作的电力系统的一些稳定问题进行了深入广泛的讨论。讨论完了,我发现对于生产第一线的电力工程师来说,电力系统稳定并不难!虽然道理可能很复杂,但在生产中,他靠几张图,就解决问题了。当然,他也挺有收获的,因为我给他画了另外几张图,告诉他,他那几张图被背后的道理大概是这个样子的。
既然人家能通过几张图把电力系统稳定弄个大概明白,我不如在这里借用一下这个方法,也许效果不错,不至于让耐心看这个帖子的人太辛苦。只不过,涉及实际系统的图被我换成了一些概念化的图。
但是,不论怎样力求简短,电力系统的数学描述总是饶不开。为了避免以后的麻烦,还是先介绍一下,点到为止。可以这样来理解电力系统:一个交流电路,加上若干个动力系统,再加上若干控制系统。交流电路包括输电网络和发电机、电动机等设备的等值电路,满足电磁场方程、基尔霍夫定律和欧姆定律,可以用微分方程和代数方程表示。动力系统主要包括发电机和其它旋转设备,满足牛顿定律,可以用微分方程表示。控制系统包括各种发电机控制设备,如励磁机、调速器等,可以用一系列微分方程描述。这样一来,电力系统就可以用下面的微分-代数方程组来描述:

上面的是微分方程,下面的是代数方程。这个代数方程实际上就是前面曾提到的潮流计算方程,是从基尔霍夫定律和欧姆定律导出来的。要准确描述一个电力系统的动态特性 ,需要有很多个微分方程,比如发电机的电磁场方程和其它控制设备的微分方程。这些微分方程中,最重要的是两个关于发电机转动的动力方程:

其中N是发电机个数,θ是发电机转子的相对于某参考轴的角度,ω是角速度。第一个方程表示角速度是角度对时间的导数,是大家都熟悉的基本运动方程。对于第二个方程,请先回忆一下牛顿第二定律:力等于质量乘以加速度。M是可以想象为发电机转动部分的质量,乘以角加速度(角速度对时间的导数),等于作用在发电机转子上的力。这个力在这里是机械功率减去电气功率。其中机械功率是由原动机作用在发电机上的,相当于驱动力,电气功率是发电机送往电网的,对发电机的转动来说是阻力。这两个微分方程定义了发电机的基本运动特性。在正常运行时,机械功率和电气功率相等,发电机转速不变(系统频率,60Hz或50Hz)。当系统中发生一个扰动,改变了发电机机械功率和电气功率的平衡时,发电机的转速就会发生变化。因为各个发电机受扰动的影响不一样,速度的变化也不一样。这样,发电机在扰动和控制设备调控的共同作用下,就会发生相互振荡。
最基本的电力系统稳定性分析方法就是对上述微分-代数方程组在时间轴上积分,也叫时域仿真。现在已经有很多成熟的软件包可以完成这个任务。其输出就是沿时间轴变化的角度、角速度等变量,还有其它的电压、电流等电气量。可以把这些输出画成曲线,系统稳定与否就一目了然了。比如说,下面这个图就是一个时域仿真得到的发电机转子角度的曲线。其中三个发电机的角度迅速增大,表明系统失去了稳定。
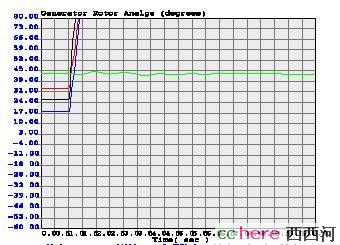
图1 失去稳定的系统`-- 发电机转子角度
对应的发电机电压的仿真结果是这样的:
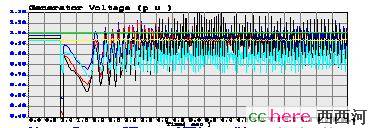
图2 失去稳定的系统`-- 发电机电压
实际上,这个系统在扰动后的第一个振荡周期内就失去了稳定,在第一张图里,可以看到那三个发电机的角度曲线一飞冲天,仿佛是飞船脱离了地球,再也没有回到我们的视野里面来。这也叫一摆失稳。对这个例子,在第一摆之后的电压仿真结果已经没有实际意义,只需要看最前面的几格。我们可以看到,发电机电压有显著下降,大概从扰动前的接近1.0降到0.6左右。
这就是从事电力系统稳定分析的工程师看到的最直观的系统失稳。问题是,一个大系统,几千个发电机,我们需要观察哪些发电机的角度或电压呢?这就需要知道系统的结构和我们所仿真的扰动的位置。下面是一个高度简化的电力系统图,用来表示从远方发电厂向负荷中心送电的情况。现实中,可以找到很多这样的系统。比如,从内蒙古煤田的坑口电厂向华北地区送电。在负荷中心,也会有很多发电机,但图中并没有表示出来。
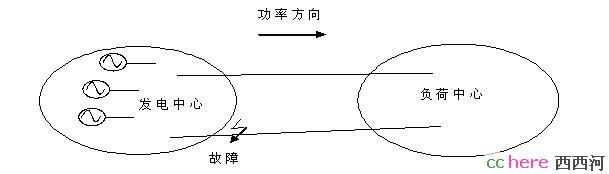
图3 电力系统
假设在发电厂出口附近的线路上发生对地短路故障,电压瞬间降到接近于零,考虑到输出功率等于电压和电流的乘积,那么发电机的输出功率也跟着突然降低。但是,发电机的输入机械功率在故障发生后并不会立刻变化。回到前面那个牛顿第二定律的微分方程:
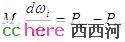
右边项的值在故障前是0,故障后就不是0了,于是发电机开始加速。与此同时,负荷中心的发电机并不会加速,反而可能会减速。这是由于远方发电厂的输出功率减少,这些负荷侧发电机需要增加输出功率以满足系统功率平衡。这样,输电线路两侧的发电机的转子角度差就会越来越大。现在,我们知道,如果仿真这样一个故障,需要看的仿真结果是发电侧的发电机角度。但由于角度是个相对值,所以实际上是看发电侧的角度和负荷侧某参考角度的差。
图1显示的系统遭受了一个非常大的扰动,导致一些发电机的角度一下子增加了很多,回不来了。在稳定性理论中,我们说这是超出了系统的稳定域。这是后话,暂且按下不表。那么,如果扰动不是那么大,会是什么结果呢?看下图。
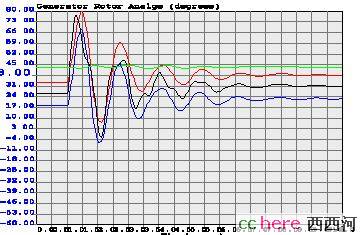
图4 稳定的系统—发电机转子角度

图5 稳定的系统—发电机电压
从图4看到,当加在发电机上的力不那么大时(实际上,还有个作用时间的因素),在电力系统自己的不懈努力下,这些发电机还是能迷途知返的。图5中的电压表现也不错。一切都归于平静,在10秒钟之后。
因为图比较多,这一部分如果放在一篇里会显得太长,想想还是分成两部分。用下面这张图先抗一下。这是一个系统仿真结果的前半部分,猜一猜这个系统的命运如何呢?
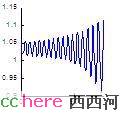
图6 系统振荡
本帖一共被 3 帖 引用 (帖内工具实现)
