主题:穷则思变富必亡 -- 给我打钱87405
- 共: 💬 116 🌺 701 🌵 3
注:这是第二讲,第一讲的内容各位自行脑补吧。😄😄😄
我为什么会坚持说,老师在黑板上画6个格子,然后告诉学生1/2+1/3等于5/6是错的,并且是有害的呢?
你会分。8个苹果两个人均分每人几个?4个。9个苹果三个人均分每人几个?3个。7个苹果三个人均分每人几个?
“呃……还有一个分不了。”
真的分不了吗?
“可以分。”
一人咬一口。
你会分,只要是长度、面积、体积、质量等等,但你不明确这一点,我的意思是说,你不明确个数、次数跟长度面积体积质量具体是哪里不同。
还有一个,你从未想过“1/2+1/3等于几”这个问题。可是,如果先让你从8个苹果中拿走一半,再让你从9个苹果中拿走三份中的一份,你一共拿几个了苹果?你会说你拿了7个苹果,这并不是1/2+1/3。
所以老师首先要明白的是,孩子其实已经知道【什么是1】了,他们知道【1】堆苹果,他们也知道【1】次投篮,他们只是没有【明确】这两者的不同。
接下来该怎么办呢?老师应该去引导学生,1/2+1/3不管等于几,我们暂且说这两个分数之和叫X,这个X一定是恒定不变的,就像1+2=3那样。因此,8个苹果的1/2是4个,9个苹果的1/3是3个,我们能说1/2+1/3=7吗?如果成立,那么8个苹果的1/2是4个,15个苹果的1/3是5个,1/2+1/3不就又变成了9了吗?所以这显然是哪里错了。
再往下的一步就非常难了,我们几乎无法想象孩子们能自己想到下面这个问题:1+2=3,这是怎么做到的?1桶水加2桶水等于3桶水,对不对?
不完全对。如果是1小桶水,再加2大桶水,我们能说一共有3桶水吗?所以1/2+1/3是不是【也】指的是有一个共同的1呢?比如说,先从8个苹果里拿走一半,又拿走8个苹果中的1/3,一共拿走了多少苹果,这个数才是1/2+1/3,对不对?
也不完全对。先从8个苹果里拿走一半就是4个,又拿走了8个苹果中的1/3就是不到3个,一共不到7个,所以1/2+1/3等于不到7?如果成立,先从9个苹果中拿走一半就是4个半,又拿走1/3就是3个,一共是7个半,怎么又变了呢?
因此,只能是老师来告诉学生,1/2+1/3到底指的是什么。
一个圆,先把一半涂上阴影,就是1/2;再把剩下的一半均分为三等分,把其中两份也涂上阴影,也就是1/3,问:两个阴影部分的总和是多少?
请注意,这里有共同的1,都是同一个圆,而不是【这1】堆苹果8个、【那1】堆苹果9个。
“两个阴影部分的总和是多少?”
相信我,孩子们几乎不可能 回答出来,只能是老师继续告诉学生:回答不出来对不对?我现在画一个大一点的圆,还是涂上两部分阴影,再把两者对比一下,有没有发现什么?还记得最开始说的吗?不管1/2+1/3等于几,这个X一定是恒定不变的。所以把这两者对比了之后,有没有发现哪里是相同的?
如果学生还是看不出来,那只能是老师告诉学生:阴影部分的占比没有变,不管圆是大还是小。
学习分数运算得先解决上面的问题。这里我要说明的是,不是反对老师引导学生,而是说几乎不可能,因为这些看似简单的问题其实难度非常高,我们人类不知道花了多少时间和精力才搞明白。可以尝试着引导,但不要抱太大指望,更多的是【告诉】学生。这个【告诉】非常重要:是我告诉你的,你自己想不出来。我也想不出来,是别人告诉我的,有智慧有勇气的人告诉我的。
把上面的问题解决之后才能进入下一环:到底怎么求1/2+1/3?
现在我们已经知道了,1/2+1/3就是指定一个共同的1,然后弄明白阴影部分占比是多少,可怎么来操作呢?
测量是可以的,在现实中有【一定】的可行性,比如早期的人类就认为圆周率是3,“径一周三”,这就是测量测出来的,但数学不会就此止步,这是为什么呢?
因为会出现误差。
“我明白了,如果一个圆的直径是1米,按测量值来看,圆周率就是3,这个圆的周长就 是3米,所以这个圆轮动100圈就是滚动了300米,但实际是314.16米,要是这个圆轮动10000圈就是滚动了30000米,但实际 是31415.93米,轮动的圈数越多误差也就越大。”
不完全对。就上述例子而言,误差并没有变大,所谓的变大指的是绝对值,可是相对值也就是百分比并没有变。真正可能的误差是这样的:π*(1/3),如果π是约等于3,1/3约等于0.3,那么π*(1/3)=0.9,这已经不是误差了,而是完全变形了,扭曲了事物的原本面目。
如果我们指定1米的绳子为1,那么1/2+1/3测出来约为0.83米,换言之,1/2+1/3=0.83,但我们不相信这个答案,因为我们已经知道了,测量是测不准的。不能测,或者说,我们必须 要找出一种方法,即便是测量也一定能测准。
把一条绳子也就是一条线段均为3等分,我们不会,对吗?可是,3倍我们会不会?我们先画出一条线段其长度记为A,然后再来3倍,其长度记为B,最后我们指定B这个长度为1,那么A是不是就是B的1/3?且一定准?
1/3是不是就解决了?1/3解决了,1/2怎么办?我来2个B,是不是解决了?我来2个B,不影响1/3,对不对?
那1/3+1/4呢?我来4个B,每个B是A的3倍,4个B我设它为1,所以1/3就是4个A,1/4就是3个A,1/3+1/4就是7个A,4个B是12个A,所以1/3+1/4=7/12。
走到这一步,才能进入“6个格子”这个环节。6个格子是指的2*3,2*3指的是两个维度,类同于一个B是3个A中的“3”是一个维度,2个B中的“2”是另一个维度。搞清楚了两个维度就省力了:用面积,长乘宽。
通过上面的讲解,大家有没有发现,“6个格子”距离 通分只有一步之遥了,并且学到这一环时已经有通分概念了,只不过还没有明确,只不过还没有纸面化运算?
所以,学校里教的不是本末倒置又是什么呢?
问:我是在讲1/2+1/3等于几吗?
我在讲怎么从【会】走向【不会】,难道还没有发现,一切的【不会】都是由若干个【会】组合到一起而得来的吗?所以我极力反对“人生下来就是一张白纸”说。
如果我是老师,我要给学生讲怎么【操作】“1/2+1/3等于几”我就直接上操作手册好了。不是这说这样就完全不可取,而是我认为100%的操作工就是机器人,我们是人类去制造机器 人,而不是把人变成机器人,对吗?所以,在我看来,最重要的就是通过这样一堂又一堂的课来告诉孩子们:你们天生就【会】,并且【会】的还不少,但你们不知道一切的【不会】都是由天生的若干个【会】组合而来的,怎么组合这就是黑科技,一开始你不知道怎么组合,所以你认为要学会【不会】就得背下来,就是大错特错。李白所说的“天生我材必有用”我认为指的就是:除天生不幸,人人与生俱来的【会】,只要学会了怎么【组合】,就能从【会】走向【不会】。
对《1/2+1/3等于几》一文的两点补充
《1/2+1/3等于几》一文中有两处需要特别关注。
一、错误和误差有天壤之别,绝不可混为一谈
用一把可信的尺子去测量房子的尺寸,一定会测不准,这种测不准叫误差;用一把粗制滥造的尺子去测量尺寸,其结果 一定是错的,错在尺子本身。正因为如此,用测量的方法去测出1/2+1/3等于多少,这一方法并不是数学的方法。只有一种测量才是数学的方法,那就是数数。人能识别出独立的物体、事件,天然就有一把可信的尺子,所以数数这一方法是可信的,但仍然有几率出现误差,数错了。
尺子是诸多说法中的一种,像道、德、准则、原则、立场、大是大非、理论这样的说法也和尺子是一样的。所以,错误和误差有天壤之别绝不可混为一谈,这是一个非常严肃的问题,这个问题本身就是尺子。但很多人对此认识是不清的,这是因为错误和误差就结果来看没有区别,【尺子错了就不可能有好结果】跟【不小心出了差子】很难分辨。比如,经常会有老师、家长指出的孩子的“错误”:马虎了,下次要注意。可怎么注意呢?实验室里的试管摔碎的几率一定大于0。我为什么会反复强调,读者读我的文章时千万不能对号入座呢?就是这个原因。人无完人指的是误差,误差是一定存在的,可很多人把“人无完人”解读成了【搞歪门邪道只要没出大事就不叫大错】,理由就是“很多人都这样”。我女儿就不理解这个问题,所以她老说“你怎么总在说我?我这也不对,那也不对?”她因此也怀疑我是故意找她的茬。而据我的观察结果来看,习惯性的故意找别人的茬,也就是有意的歪曲、扭曲(不仅指诋毁,还指“褒奖”)他人的人并不是多数,多数人的问题就出在分不清错误和误差的巨大区别。
这里顺带说一个问题,那就是所谓的物质和精神。现实中的尺子是不可能完美的,那你能不能说这叫错误而不叫误差呢?恐怕我们不能这么说,因为理论中的尺子对的就是精神,现实中的尺子是精神与物质的结合,现实中造不出来完美的尺子这叫误差,用这不完美的尺子去测量一间房子的尺寸一定测不准这还是叫误差。
二、人的学习劳动一定是从【会】走向【不会】
人的学习劳动一定是从【会】走向【不会】,这同样是一个决定生死的根本问题,然而不幸的是很多人又弄错了,他们认为人生下来就是一张白纸。我之前也曾经说人的可塑性非常强,女娲造人就是捏泥巴,玉不琢不成器说的也是捏泥巴,可再怎么捏也跳不出如来佛的手掌心,无论如何捏的是泥巴,尽管后来呈现在人们面前的是一只精美的瓷碗。
人发生学习劳动就是在塑造人,人就是泥巴,泥巴天生就自带它固有的属性,人天然就【会】,并且还【会】很多。比如我们所有人,只要是健康的,天生就会数数。而数数是数学的起点,所以我经常说,其实人人天生就是数学家。那么“人人天生就是数学家”这样一种说法是不是今天流行的“自信学”呢?“自信学”是在指鹿为马,一切“自信学”都从根本上否认了人天生就【会】并且【会】的还挺多。想想看吧,如果人天生不会数数,没有这样的与生俱来的可信的尺子,人类是不是早就灭亡了?
从【会】走向【不会】我们要注意两个要点:第一、你【会】,但你不知道。比如人天生就会模仿,人类的婴儿如果是狼给带大的,那么他的言行举止就会跟狼一样;又比如人(非常有可能)天生就懂得数量关系式,脑子里天生就有未知数X。你【会】但你不知道,对你而言这是巨大的损失,对有心人而言这就是巨大的宝藏(指走正道的有心人)或者是巨大的财富(指走邪路的有心人)。第二、【不会】是由若干【会】组合而来的,怎么组合是需要我们重点关注的。跟别人学什么?跟前辈学什么?跟睿智的人学什么?学怎么组合。
举个例子来说明【组合】:把任意一条线段AB三等分,你是不是不【会】?可如果我要说你【会】呢?你是不是不相信?
放大3倍你会吧?相似三角形你会看吧?这俩是你天生就【会】的,对吗?所以有:
过线段AB的其中一个端点A做一条射线AC,任取一个长度记为(单位)1,将(单位)1在AC上首尾相接的复制3遍,这样得到三个点,记为D、E、F,AD=DE=EF。连接点F和点B得到线段FB,过点E做直线平行于线段FB且与线段AB相交于E1,再过点D做直线平行于线段FB且与线段AB相交于D1,E1和D1就是线段AB的三分点。图如下:
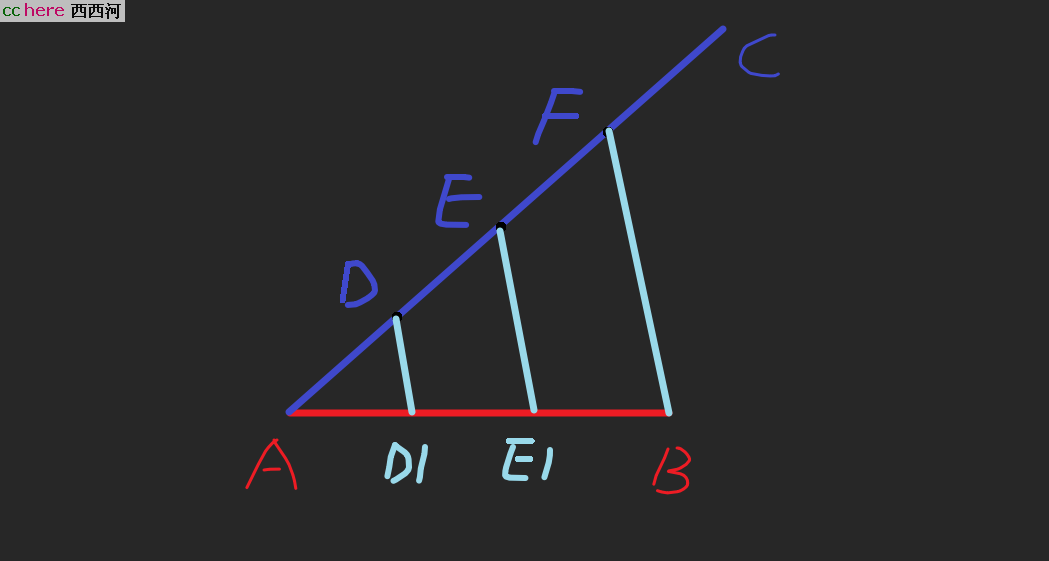
如果你说“这也太难了吧”,那么我需要告诉你的是:你天生会什么,我天生的跟你一样,可你始终活在猛犸象时代,我已经遥遥领先于这个时代了(指平均发展水平),你的命运就是所谓的被时代抛弃了,需牢记【行有不得,反求诸己】啊。
最后来看一条新闻。
看完这篇报道你可能会急,但请你不要急,想想【行有不得,反求诸己】。“反求诸己”并非总是指自己错了,而是指没能解决问题。报道中开锁匠的妻子是提出赔偿,赔偿的意思有过错的一方向无过错一方支付一定数额的金钱或者别的,如果她不这么做呢?如果她提出的是申请,申请抚恤金或者奖励(见义勇为奖)呢?
由于我这是假设,我并没有找到成功的案例,所以我的看法是这样形成的:官方机构自有他的程序或者说制度也行,对吧?这不像个人,你同意就同意了,对吧?所以开锁匠的妻子赔偿我认为是不可能走得通的。
或许你会问,“依你这么说,那相关部门的相关人士理当教这位开锁匠的妻子啊!”所以这篇报道并不完整,至少有两种可能:一、有人教,但开锁匠的妻子不同意,可能是因为金额问题;二、没人教,这确实是不作为,但这是另一个问题。如果是第二种可能,那就意味着两个环节都出了问题,开锁匠的妻子那边处理不当,相关部门这边也问题,组合在一起就发生了“变形”,让整个事件以扭曲的形态呈现在大家面前。
我想提醒大家的是,如今是信息爆炸的时代,我们每天都会阅读很多新闻 报道,然而这些报道往往是不完整的,在这样的情况下,如果你随便一读又轻率得出一个结论,我可以负责的告诉你,日积月累之下,你要么就是消沉,要么就是被愤怒所支配,无论是哪一种都是致命的。
- 相关回复 上下关系8
🙂不用猜了,看来您不是物理专业的 7 Swell 字1215 2023-12-10 14:18:54
🙂最著名应该是电阻和电导率 7 假日归客 字249 2023-12-11 02:49:06
🙂我的一个畅想 5 给我打钱87405 字3296 2023-12-11 00:39:42
🙂1/2+1/3等于几

🙂行有不得,反求诸己 5 给我打钱87405 字14042 2023-12-07 11:40:14
🙂再再再说人心无法证明 1 给我打钱87405 字12409 2023-11-30 03:51:41
🙂人剑合一 8 给我打钱87405 字29478 2023-11-27 04:36:25
🙂等高线拾遗 7 给我打钱87405 字11366 2023-11-26 04:37:59