主题:【原创】勾股定理(七)--- 做人要低调 -- 我爱莫扎特
与高斯智力上的“高调”相伴相随的,是他性格上的“低调”,“低调”得令无数人咬牙切齿。
高斯发表的作品已经无人能及,而他还有大量未发表的工作记录在笔记本内。从20岁开始,高斯一直坚持记科学笔记,直到去世。此后,后人研究他的笔记,并花了近50年时间加以整理。整理的结论令人震惊!人们发现高斯生活的时代大部分重要的数学工作几乎都是高斯首先发现的,而他却秘而不发,让许多数学家重复劳动。难怪后来有人评价说,如果高斯合作一些的话,数学至少可以加快五十年的步伐。
高斯的低调源自两方面,一是德国人的性格使然:沉默,严谨,对工作的完美主义倾向。那个时代的许多德国科学家都有不轻易发表论文的习惯。而法国人似乎正好相反。高斯的学生黎曼(Riemann)和同时代的法国大数学家柯西(Cauchy)就是一对典型的例子。40岁就英年早逝的黎曼,对数学做出极大的贡献,可他一生只发表了6篇论文,可谓字字珠玑。而柯西的论文却又多又好,据说法国科学院由于柯西的存在,一度对其他数学家论文发表加以限制,以保证柯西的论文能及时付印。高斯本人无疑是完美主义的典范。对高斯而言,如果一项成果不能做到至善至美,他绝不愿意发表。而且即使发表,他只保留最精华的部分,并将一些在他看来“多余”的部分抹去。所以高斯的作品发表后,通常要由其他比他差一些的数学家(往往是他的学生)加以诠释,才能让普通的数学家读懂。
另一方面是高斯特有的高傲和敏感。高斯初出茅庐时,和所有有创新精神的年轻人一样,作品受到权威的批评。可那些权威们的水平比起高斯颇有差距,不少批评很无厘头。要是牛顿同学遇到这样的情况,多半会跳将出来,挥舞大棒逐个反驳。可高斯却选择“不玩儿了”。今后的他,对于不成熟的新发现多半选择不发表以避免争议,或者用深奥的数学语言层层包裹,使得他的论文著作非真正的专家不能读,避免一切民科的骚扰。高斯21岁时写就的名著《算数探究》就是这样一本“天书”,被人称为“加了七道封印”的书(全书共七章),直到今天都令人望而生畏。
可以想象像高斯这样的大人物会招来多少民科。以高斯怕麻烦的性格,他对民科一向不怎么待见。有个关于高斯蔑视民科的小八卦。曾有人问他牛顿被苹果砸的故事,身为同样等级的科学家,高斯非常明白牛顿工作之伟大卓绝和发现过程之艰苦。据说高斯听了这个故事,当时就发了飙:“愚蠢!如果你愿意,就相信这个故事好了。但事情的真相是这样的:一个愚蠢的、爱管闲事的人问牛顿,他是怎样发现万有引力定律的。牛顿看出他是在跟一个只有儿童智力水平的人打交道,便想避开这个讨厌的家伙,于是就回答说,有一个苹果掉下来,打在了他的鼻子上。那个人完全明白了,非常满意地走开了。”
可怜的伽罗华和阿贝尔也被高斯误认为是民科,实在令人扼腕叹息。
低调的性格加上巨大的创造力,造就了“高斯的笔记本”。据他自己回忆,他在20岁左右的那几年,太多太多的新思想占据着他的头脑,让他无所适从,不知道应该先研究哪个,只好把它们先记录下来。在几十年的时间里,他的笔记里记录了大量不成熟的,尚未深入加以研究的崭新的思想。这些思想有不少被其他数学家再次发现,并加以发展,最终形成理论。由此引发的口水仗不胜枚举,而高斯与小鲍耶的非欧几何恩怨无疑是最著名的。
早在20岁不到的时候,高斯就曾经尝试证明第五公设,并和其他人一样,一度以为自己成功了。过了几年,高斯终于意识到自己的错误,并率先发现了非欧几何。不过他从未发表自己的发现,只是在和友人的通讯中提了一句。甚至在他的笔记里也没有详细的记录。

此后,鲍耶和罗巴切夫斯基做出他们的发现后,高斯也从未给予公开支持。高斯在给老鲍耶的信中以长辈谈论小辈的语气,写了那几句让小鲍耶暴跳如雷的点评。这样对待年轻人实在太不厚道,尽管高斯从来对年轻人都不太厚道。(他偶尔也表扬年轻人,但确实很少)罗巴切夫斯基在俄罗斯饱受批评,高斯帮助他得到了德国的通讯院士职位,自己还学习俄语研究他的论文,却仍然没有公开发表过对其发现的支持。
为此,高斯饱受诟病。不少后人认为高斯的保守和胆小减缓了人类的进步。在我看来,这话有一定的道理,但远远不是全部。高斯的性格确实不喜欢卷入任何争论,而非欧几何又是一个巨大的漩涡,让其本能的想避开。但就此评价高斯保守胆小,实在有些偏颇。高斯的一生,打破的教条之多,做出的惊人发现之多,少有人比。正是高斯,将人们长久以来视为“幽灵”的虚数正式引入数学,并对其认真加以研究。如果说高斯胆小的话,只怕没有几个科学家能被称为勇敢了。
我相信,在高斯的性格原因之外,还有更深刻的原因。那就是,高斯相信当时的人们,甚至包括他自己和鲍耶,罗巴切夫斯基,其实并没有真正理解非欧几何。欧式几何也好,非欧几何也好,如同露在海面上的冰山一角,而高斯显然对隐藏在水面下的冰山更有兴趣。所以,高斯的沉默其实很简单:在彻底搞明白之前,他不愿发表不成熟的意见。仅此而已。
事实上,穷其一生,他对整个几何学的探索从来没有停止过。上帝没有辜负他,在他去世前不久,他幸运的瞥了一眼海面下的冰山,终于对非欧几何有了满意的答案。而这个答案正是建立在高斯一手创造的新王国 --- 微分几何的基础上。
本帖一共被 2 帖 引用 (帖内工具实现)
眼下,在中国学术圈子里,像高斯这样行事的人我见的是越来越多,这只能说是中国学术水平越来越差的见证。
对一个科学工作者而言,尤其是数学家,博士毕业后的头十年特别重要,很多创新的想法都是在那个时候形成。所以一个好的学术体制必须鼓励年轻人。
美国采用的tenure制度,保证了成名的大教授享有优厚的待遇,而不必压制年轻人搞恶性竞争。当然,年轻人刚毕业时压力还是会很大。
而法国为代表的欧洲的许多国家,虽没有很优厚的待遇,却能让大多数年轻人得到稳定的工作,使他们可以静下心来做基础研究。避免了阿贝尔的悲剧再次发生。
两种体制各有利弊。中国似乎还在探索自己的道路。
压力有时候还是必须的,尤其刚出道的时候。我同意黄金十年的说法,tenure考察期也有六七年长,也不算短了。这段时间,一方面是要reveal他的真实实力,也是在塑造一个junior faculty的研究习惯,这样tenure以后,也会习惯成自然地继续研究,因为这已经成为人生价值的体现,这是内力,外在的,还有学术声誉的促进。
tenure期间逼你出全力,tenure以后允许你天马行空。
查你的全部帖子都找不到。
本文的主题是“勾股定理”,但被我天马行空的写成了几何学发展史,是我自己也料想不到的。不过,这背后的原因并不难理解。勾股定理无非是计算长度(或者说距离,度量)的公式,而测量长度从来就是几何学的根本。
让我们看看什么是“几何”。Geometry这个词,分为两部分。Geo代表大地,来源于希腊神话的众神之母 --- 大地女神盖亚(Gaia)。话说盖亚诞生于世界最初的混乱状态(卡俄斯,Chaos),是第一个希腊古神。她生下天空之神乌拉诺斯,又与他结合生下了众神。现在掌权的宙斯是她的孙子。。。对相关历史感兴趣的同志可参阅Hesoid写的纪实报告文学《神谱》(Theogony)。另一方面,metry与mesure,metre等词同源,意为测量。Geometry者,大地测量也。
远古的农耕时代,为了精确计算土地的长度和面积,人们渐渐摸索出一套研究各类图形的方法,这就是欧式几何学的来源。渐渐的,几何学脱离了土地,变成了一门纯粹的“公理化”的数学理论。后人们清楚的记得阿基米德去世前的场景:当他的城邦被罗马人攻破时,他正在沙地上潜心研究几何,一名闯入的罗马士兵踩坏了地上的图形,让他怒不可遏,与其争执,而不幸被刺,倒在了他最钟爱的几何图形上。
此后近两千年,数学家对天空的兴趣似乎远大于大地。与阿基米德同样伟大的牛顿从天空得到灵感。在研究行星轨迹的问题上,他发现了万有引力定律,并独立发展了微积分这一人类有史以来最有力的数学工具。
1818年,在经历了早年在天文学领域的辉煌后,高斯把目光重新投向了大地。在此后的九年时光里,他主持了汉诺威公国的大地测量工作。这不仅是地质测绘史上的重要工程,也开启了几何学新的一幕。
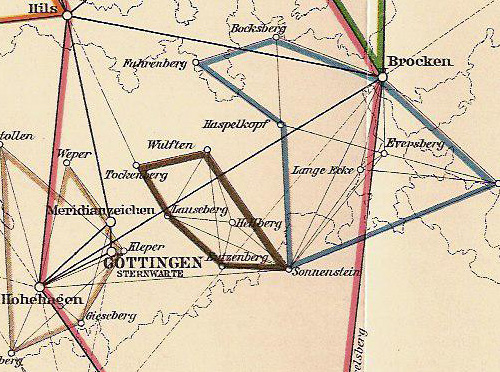
作为一个纯粹的数学家,高斯主导这样一个“实际”的工程一定有他自己的道理。在我看来,非欧几何应该是驱使他测量大地的动力之一。测量过程中,高斯曾试图通过测量Harz的Brocken --- Thuringer Wald的Inselsberg --- 哥廷根的Hohen Hagen三个山头所构成的三角形的内角和,以验证非欧几何的正确性。很可惜,测量的精度不够,实验未成功。但这说明高斯这个非欧几何的先驱一直相信我们生活的宇宙不是欧式空间。如果实验成功,非欧几何便不再是想象的几何,而是实实在在的大自然的几何学了。事实上,高斯,罗巴切夫斯基,鲍耶以及后来的黎曼,始终致力于寻找非欧几何的物理意义。他们无疑是有先见之明的。
在公开资料中,对高斯的大地测量工作描述如下:
高斯亲自参加野外测量工作。他白天观测,夜晚计算。五六年间,经他亲自计算过的大地测量数据, 超过100万次。当高斯领导的三角测量外场观测已走上正轨后,高斯就把主要精力转移到处理观测成果的计算上来,并写出了近20篇对现代大地测量学具有重大 意义的论文。在这些论文中,推导了由椭圆面向圆球面投影时的公式,并作出了详细证明,这套理论在今天仍有应用价值。汉诺威公国的大地测量工作直到1848 年才结束,这项大地测量史上的巨大工程,如果没有高斯在理论上的仔细推敲,在观测上力图合理精确,在数据处理上尽量周密细致的出色表现,就不能完成。在当 时条件下布设这样大规模的大地控制网,精确地确定2578个三角点的大地坐标,可以说是一项了不起的成就。
这段描述让我们了解到大科学家的过人之处。
首先,是勤奋的工作态度。古来有大成就者,无一不是经过长期艰苦卓绝的工作。即便像牛顿,莫扎特这样举世公认的天才,如果人们了解他们的工作时间和状态,就不会惊讶于他们的巨大贡献。所谓“牛顿的苹果”或者“瓦特的水壶”,演义的成分远远大于真实性。荀子曰:“不积硅步,无以至千里。不积小流,无以成江海”,汉诺威的大地测量正是在高斯的手中一个数据一个数据测绘而成。
光靠勤奋成不了大师。人类与动物的区别,在于人类会使用和创造工具。而科学大师则是那些最善于使用工具和发明工具的人。

阿基米德发现的浮力定律,杠杆原理,积分等等数学物理学工具,大大提高了人类的生产力。而他还喜欢自己发明制作机械。他不仅发明了举重滑轮、灌地机、扬水机等民用设施,还曾经把他的科学知识运用在国防事业上。他所在的小城邦几乎依靠他一人之力击退了多次罗马人的进攻。传说中,他运用杠杆原理设计的投石机击退敌人无数,运用光的反射制造的聚光镜曾将敌船焚毁,他甚至还发明了铁爪起重机将敌船抓起掉转。

牛顿为了研究天体运动,一手打造了数学工具 --- 微积分理论。微积分为后来的第一次工业革命奠定了理论基础,可谓人类有史以来最重要的数学工具。而牛顿为了自己的研究也经常亲手打造工具。他为了观测天体而制造望远镜,自己设计了研磨抛光机,实验各种研磨材料。不久,他制成了第一架反射望远镜样机。

在汉诺威公国的大地测量中,高斯动用了一切能动用的工具。为了测量的需要,他发明了日光反射仪。为了进行大规模的数值计算,没有计算机帮助的高斯充分运用了他发明的最小二乘法和快速解线性方程组的算法,他的这套方法直到今天仍被计算数学(又称数值分析)的专家们广泛使用。最重要的是,他对地球表面的研究最终形成了现代微分几何学。
高斯的微分几何不是一两句话能讲清楚的。打个比方:欧式几何学好比中国古代的武术,精美绝伦又技巧繁复。而笛卡尔的坐标几何以及牛顿莱布尼茨的微积分则如同火器的发明。高斯的微分几何相当于教会了古战场上的人们如何使用火器。自此,几何王国完完全全改朝换代了。
接下来的一段时间里,我会把微分几何的一些重要的内容独立成章,补充在这节后面。其中不可避免的会出现一些技术性的内容,我会尽可能加以解释,相信了解一点微积分的朋友们能不太费力的看懂它们。
本帖一共被 4 帖 引用 (帖内工具实现)
高斯在那儿工作到最后一刻
艺术品
看了居然鼻子有点酸酸的。
高斯是德国精英最杰出的代表,从他的身上可以看出这个国家为什么在将近一百年的时间里站在世界的最前沿。
最近在认真的学习数学
我的理解,高斯的两个贡献
一,代数基本定理,而伽罗华证明五次以上代数方程一般不可能求解是建立在高斯的这个定理的基础上的,然后伽罗华在这个基础上建立了群论。
二,几何,高斯发现了曲面具有的独特的性质,从而开辟了几何研究的新方向,后来被黎曼,嘉当 陈省身等人发展----陈省身的工作的成就到底有多大,不清楚,我看过有的评论是美国几何的振兴是由陈省身来到美国开始的,丘成桐现在研究的微分拓扑---什么卡拉比--丘流形等等,他也是这个领域的一位非常重要的人物了
我认为彭加勒是可以与高斯相比的一个人物