- 近期网站停站换新具体说明
- 按以上说明时间,延期一周至网站时间26-27左右。具体实施前两天会在此提前通知具体实施时间
主题:【原创】素数狂想2000年 -- lucase
本文原为山东大学数学院刘建亚院长为数学系基地班的新生所作的演讲。现整理并补充相关的资料后集结成篇。
素数狂想2000年
2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59,61,67,71,73,79,83,89,97,101,103,107,109,113 这些数是什么数?对,他们有一个共同的名字——素数
伟大的德国数学家高斯(Johann Carl Friedrich Gauss 1777年4月30日-1855年2月23日)外链出处曾经说过,“数学是科学的女王,数论则是数学的王冠。”
18世纪最伟大的数学家约瑟夫·路易斯·拉格朗日,(Joseph-Louis Lagrange,1736年1月25日-1813年4月10日)在数论和数学的其他分支以及物理学和天体力学方面都做出过重要的贡献。当他在研究出“每个数都是四个整数平方和”这个定理之后说,“对我来说,算数(数论)是最难的。”
法兰西科学院院士Jacobian说过,“上帝是算数学家。”
“数统治宇宙”
数统治宇宙这样狂的话,出自古希腊最著名的数学家——毕达哥拉斯外链出处。毕达哥拉斯在雅典创建了毕达哥拉斯学派。他对自然数、分数、有理数等各个领域都做出过杰出的贡献。他还曾经用整数的比例问题来研究音乐中的和弦问题。
罗素曾经这样评价过毕达哥拉斯,“我不知道还有什么别人对于思想界有过像他那么大的影响,我所以这么说,是因为所谓柏拉图主义的东西倘若加以分析,就可以发现在本质上不过是毕达哥拉斯主义罢了。有一个只能显示于理智而不能显示于感官的永恒世界;全部的这一观念都是从毕达哥拉斯那里来的。如果不是他,基督徒便不会认为基督就是道;如果不是他,神学家就不会追求上帝存在与不朽的逻辑证明”。但是当毕达哥拉斯发现 圆周率、开方2 等无理数时,大为震惊。他的学生 Hipparsus of Tarentum 向外人透露 无理数 的存在,其后便给毕达哥拉斯淹死了。不知道这算不算最早的学术迫害。
讲过以上这些以后,我们不得不认识到,有一类数在数学的研究中有着基本的重要性,那就是素数。在此我们不可避免的要提到素数的定义:素数,又称质数,一个大于1的自然数中,除了1和此整数自身外,没法被其他自然数整除的数;即是只有两个正因数(1和自己)的自然数。如果我们有兴趣查看一下素数序列的话,就会发现其中唯一的偶数2,而其他的素数则都是奇数。素数是构成全体整数的基本元素,任何一个正整数都能写成素数方幂的乘积。比如2385就可以分解成3的平方,5的平方和11的平方的乘积。
那么在知道了上述的情况之后,我们会问,素数在整个整数序列中是如何分布的呢?如何判断一个整数数否是素数呢?
早期的数学家们的实验结果让人很沮丧,基本上属于数手指头的方法。我们只能通过检验一个数是否可以被前面的整数整除。但是当这个数非常大的时候,使用这个方法的结果大概只有崩溃一条路可走了。
如果我们查看前人留下的素数表的话会发现,素数的分布是没有规律可以遵循的。素数的分布是一个随即的过程。所以曾经有人试图找到一个能够源源不断的产生新的素数的通项公式。当然结果是失败的。但是令人欣慰的是,我们可以找到一个很简单的证明这个想法是错误的方法。
如果从整个数轴的角度考察素数的分布,我们无异于大海捞针。那么我们可以取一个(0,x)的区间,考察这个区间内素数的分布情况。当然,这个X也是趋于无穷大的。但是尽管X趋于无穷大,却怎么也追赶不上数轴的箭头,所以X总也跑不到头。那么,我们记(0,x)这个区间上素数的个数为π(x),在此用π来标记素数的个数是因为π这个希腊字母对应的拉丁字母是P,而P正好是素数这个单词的第一个首字母。那么,我们可以得到这样的结论,随着x的逐渐增大,π(x)也是随之发生变化的。
我们又不可避免的要提到另外一个伟大的古希腊数学家欧几里德(约前330年—前275年)外链出处他的《几何原本》被誉为影响人类历史的三部著作之一。另外的两部,其中之一肯定是bible了,还有一本,不清楚。欧几里德对素数理论的贡献是,他证明了整数集中包含了无穷多个素数。
欧几里德

说完了素数的一些基本概念,我们要开始看素数定理了。
先看一下素数定理的定义外链出处:对正实数x,定义π(x)为不大于x的素数个数。数学家找到了一些函数来估计π(x)的增长。以下是第一个这样的估计。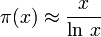
其中ln x为x的自然对数。上式的意思是当x趋近∞,π(x) 和x/ln x的比趋近1。但这不表示它们的数值随着x增大而接近。
如果我们注意这个公式的一个推导,π(x)/x = (x/lnx)/x = 1/lnx →0 暨素数的密度为0.那么我们可以看出,在整数序列中随机选择一个整数,它是素数的概率趋向于0,因此素数是特别稀疏的。
这个最早的推测是由德国数学家高斯和法国数学家勒让德(Adrien-Marie Legendre,1752年9月18日–1833年1月10日)完成的。
让我们再多说几句高斯。在知道高斯这个名字之前,我不相信数学界真的有天生奇才这种说法。直到有一天,我知道了高斯。高斯在12岁的时候(12岁的时候我们在干吗?)就知道要用同余式来统一整个的算数。15岁的时候就推测出了素数定理,但是很遗憾,他无法给出证明。
伟大的高斯

法国数论家勒让德

高斯是世界上为数不多的几个被印在钱上的数学家。
前联邦德国10马克

接下来我们会继续讲切比雪夫等同志是如何围绕数论展开研究的……
看了这篇,不禁想起了qiaozi兄的长作链接出处
只可惜他没能给续上。
深受感动,懊悔当初怎么没学数学呢![]()
粮票用完了,先欠着。![]()
看完上面的内容,我们可以得到下面这个不精确的结论:几乎所有的整数都不是素数。
俄国数学家,切比雪夫(俄文原名Пафну́тий Льво́вич Чебышёв,欧洲语言译名有Chebyshev, Chebychev, Chebyshov, Tchebycheff, Tschebyscheff等。 (1821年5月26日-1894年12月8日),俄罗斯数学家。)[URL=][/URL]证明了上面我们所提到的那个π(x) 和x/ln x的比,确定地在0.99和1.11之间。这个证明使用的依然是初等数学的方法,但是非常有效。
切比雪夫的画像

切比雪夫曾经长期的生活在圣彼得堡的俄国科学院。他除了在数论方面有研究外,对于逼近论也有研究。当然,他的切比雪夫不等式,也很有名。
但是很遗憾,切比雪夫的方法,依然是属于数手指头的方法。无法真正精确地证明素数定理。
一个伟大的联系
我们终于要开始讲到黎曼了。
黎曼的画像

格奥尔格·弗雷德里希·波恩哈德·黎曼 (Georg Friedrich Bernhard Riemann,1826年9月17日 - 1866年7月20日)德国数学家,对数学分析和微分几何做出了重要贡献,其中一些为广义相对论的发展铺平了道路。他的名字出现在黎曼ζ函数,黎曼积分,黎曼引理,黎曼流形,黎曼映照定理,黎曼-希尔伯特问题,黎曼思路回环矩阵和黎曼曲面中。外链出处
在此我们不得不提到德国哥廷根大学严格的教授评审制度。伟大的高斯曾经担任过哥廷根天文台的台长和哥廷根大学数学教授。高斯去世以后,狄利克雷(Dirichlet)接替了高斯的教授职务外链出处,八年后,狄利克雷去世,这次才终于轮到黎曼担任数学教授的职务。此前他只能以编外教授的身份待在哥廷根。(黎曼这个超牛在大牛去世前也只能担任编外教授,对比一下今天的情况,真是汗颜。)
在此我们一次次的提到哥廷根这个名字,是有原因的。哥廷根大学外链出处的数学曾经照亮了整个人类世界,从高斯和黎曼到克莱因和希尔伯特。可以说,二战以前的数学,很大程度上都是哥廷根的故事。而二战以后的数学,很大程度上都是普林斯顿的故事。
黎曼的一生只发表了十几篇论文。当然这些论文如果是在今天这个年代发表的话,被SCI……等等收录是肯定的了,影响因子肯定也要高的吓人。黎曼在晋升教授的时候,撰写的论文的题目是《论不超过一个大整数的素数的个数》。黎曼在这篇横空出世的文章中,首次建立了这样一个伟大的联系:把离散的素数分布的问题跟一个连续的函数联系起来,这个函数是一个复参量函数。当然这个函数在复平面的局部是由一个无穷级数定义的。这个无穷级数绝对一致收敛的时候,就会收敛到一个解析函数。用一个连续的函数去研究一个无穷级数的量,这里面有着非常深刻的洞察力。这是一件很不得了的事情。为什么有的学科看起来就怎么也用不上数学,为什么有的学科就怎么也深入不进去,就是缺少像黎曼这样的大数学家去研究那个学科。这种伟大的联系建立不起来,所以就总是停留在用数手指头的方式上来进行研究,自然也就没有进展可言。当然,这种伟大的联系在数学史上都是可遇而不可求的。黎曼,就是这种稍有的奇迹之一。
黎曼在他晋升教授的论文中,证明了黎曼ζ函数ζ(s)有无穷多个零点,而这无穷多个零点又都落在一个无穷的带型中间。
这无穷多的根,关于1/2这条线是对称的,而且这些根都落在(0,1)这个区域向y轴正反两方无限延展的带型中间。黎曼认为,如果在这个带型的两个边上没有根的话,就能证明出伟大的高斯和勒让德所猜测的素数定理来。多说一句,素数定理是整个数论的中心定理,也是整个数学的中心定理之一。黎曼进一步猜测,如果这些根能够全部落在1/2这条线上的话,那么就会出现最好的情况。如果果然如此,那么素数定理就会有一个非常美丽的形式,而且美到了最佳。既然上帝是算术学家,那么这个猜测就必然是正确的。
素数定理的证明
黎曼规划了素数定理证明的途径,但是在当时没有相应的可以使用的证明工具。黎曼在39岁就去世了,真是天妒英才。但是,我们的目标一定要达到,我们的目标一定能够达到!
证明素数定理的是一位法国的数学家,雅克·所罗门·阿达马(Jacques Solomon Hadamard,1865年12月8日—1963年10月17日)外链出处和比利时数学家Charles Jean de la Vallée-Poussin。阿达马除了证明素数定理之外,还做了很多有益的工作,在函数论上广有建树。实际上,从黎曼的论文提出这个猜想到阿达马论文的发表,中间经历了50年的时间。这50年间,阿达马和de la Vallée-Poussin都在不停地发展用于证明黎曼猜想,实现黎曼的伟大宏图的工具。
另外阿达马还是早期访问中国的外国数学家之一。他早年间曾到清华大学做演讲,当时华罗庚先生正在清华做图书管理员。华先生把论文拿给阿达马看,阿达马建议华先生如果想要研究数论的话,应该去找哈代,于是华老1937年到了剑桥,这才有了后来中国数论一系列的发展。
Jacques Solomon Hadamard和Charles Jean de la Vallée-Poussin两人各自独立地证明了黎曼猜想,两人的论文均在1896年发表。无论如何吧,素数定理被证明出来了,大家应该为之高兴。
后面我们再讲黎曼猜想……
老人家竟然可以用心算完成线性回归分析,神!
像我等凡人还是不要跳这个大坑了,这是绝对没人填的了的坑
http://www.maths.bris.ac.uk/~hb0262/Collection/Mathematics/mathematics.htm
居然一年过去了,对不起大家,汗
而且也是复参量函数。
尤其是数论……