- 近期网站停站换新具体说明
- 按以上说明时间,延期一周至网站时间26-27左右。具体实施前两天会在此提前通知具体实施时间
主题:【原创】勾股定理(九)--- 坐标 -- 我爱莫扎特
坐标的发明,是数学史上值得大书特书的历史性事件。这个简单而不平凡的工具,彻彻底底的改变了几何学的风貌。
坐标,是一座桥梁,将“形”和“数”完美的结合了起来。有了它的帮助,我们可以把纯粹的几何问题转化为代数的计算。许多曾令人耗尽脑汁的几何难题突然迎刃而解。欧式几何这门人类最古老的数学分支之一,在坐标诞生之后,即被人类彻底征服。
不仅如此,在计算机发明之后,人类更是开始探索“机器自动证明”方法。20世纪七十年代后期,中国数学家吴文俊通过研究代数方程的性质,在平面几何的机器证明上取得一系列重要突破。用他的方法,不仅能证明已有的几何定理,还能发现新定理。此后,欧式几何不仅对人们不再困难,连机器都可以轻松搞定。

坐标的思想如此简单,让人很难理解人类为何花了那么久的时间才掌握它。其实,坐标思想的雏形,大概早在千年之前就有,但当时的人们对代数计算的掌握远远谈不上充分。直到距今350年前,法国大数学家,大哲学家笛卡尔(Rene Descartes)终于能熟练掌握今天高中生所熟知的那套数学工具,从而将人们一直朦朦胧胧略有了解的坐标思想清晰的表达了出来,一举奠定解析几何的基础,也为后来的微积分提供了成长的土壤。
而且,笛卡尔坐标系的思想在代数学领域也得到了很大的发展,为了研究高维欧式几何,必须发展对应的代数工具,这就是今天理工科大学生必修的“线性代数”。
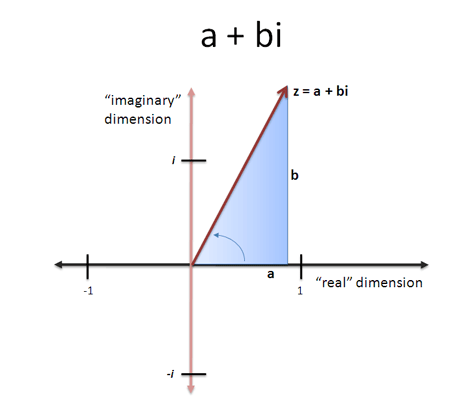
这种“形”与“数”互相转化的思想简明易懂,人们似乎早已习惯而感受不到它的伟大之处。但伟人的心灵似乎是相通的。与前辈笛卡尔一样,高斯非常清楚坐标的力量。笛卡尔用坐标将“形”转化为“数”,而高斯则用坐标将“数”转化为“形”。在人们对复数(即实数加上虚数)还心存疑虑的时候,高斯第一个提出可以将复数看作平面上的点。这样一来,对复数的研究很容易转化为对几何的研究。这个简单的思想,直接改变了此后近200年整个数学的面貌。
此后,高斯的思想被他的学生黎曼进一步深化。为了研究复变函数(即以复数为自变量的函数,这类函数与实变函数差异很大),黎曼经常考虑函数的几何性质。作为一个典型的例子,可以参看我爱莫扎特:【原创】看得见的数学之Mobius变换

由于复变函数的特殊性质,黎曼还特地发明了一种几何对象 --- 黎曼面(Riemann Surface)。这或许是20世纪数学家最喜爱的几何对象了吧。它的影响甚至超出科学之外。不少艺术家以此为题作画,比如Escher的名作《画廊》(Print Gallery)就是画在黎曼面上的。
[MP=480,480]http://escherdroste.math.leidenuniv.nl/clips/bclip_1_1.mpg[/MP]
更有甚者,Aldous Huxley在小说《美丽新世界》(Brave New World)中,有种流行的体育运动叫“黎曼面网球”,想必是非常困难的运动。
======
好久没更新,实在是自己的事情很忙。坐标这篇本来打算写到微分几何的局部坐标系,不过写得太长了,就先贴一半上来,剩下的已经接近完成,很快贴上来。
另外,感谢河友支持我成为认证会员。也请大家积极回复,告诉我你们的意见。
本帖一共被 2 帖 引用 (帖内工具实现)
Goedel, Escher, Bach是最近几年看过的最令我激动的一本书,里面好几个问题都是我小时候就开始迷惑不解的,看到有大师address同样的问题,有心意相通的爽的感觉。
为Escher就当献花一朵。
我在高中时买过一本中文版,厚厚的一大本,很有趣的。
埃舍尔的画真是神奇,里面有很多数学,而他自己好像只有高中文化水平的说。
不过,你高中就看过啦,我是今年才翻开的,你早我十年了!不过那时候没听过那么多Bach,数学也不算好。
与时俱进的艺术家就是要承受受数学的强烈感官冲击并把他传递给大众。
这个论断貌似微言大义啊。
给咱们举几个与时俱进的例子?
俺高中开始看,但一直没看全。。。
这本书确实很有名,中文版就有两个,第一个版本是摘译,叫《永恒的金带》。后来商务出了完整的版本,改叫《集异璧》,玩点小文字游戏。原书有很多文字游戏,又往往与主题相关,翻译确实很困难。
老喜欢里面那只乌龟的。
我这番微言是在纽腰的那个盘了一圈又一圈的博物馆里发生的。和一帮附庸风雅朋友去看一个现代画展。那时和老婆大人正处在人背后拉拉小手的阶段。眼红老婆大人和某雅人在一片涂鸦间相谈正欢,憋出来的。
经过了老婆大人多年的培养,发现这个微言还是巧合大义的。艺术的两样功能,自由表达和非理性途径的教化。表达的是内心和对外部世界的认识,那么在科学昌盛的今天山顶洞人艺术家必不是艺术表达的全部。(说句题外话,孩子和傻子都有艺术家的表现力,因为他们的表达方式尚未被训练和压制。)说到非理性徒径的教化,您看看老胡就知道怎么回事了。胡丹青:深有同感!
举个几个例子,现在电影艺术的CG做的不错啊。我进电影院看的就是这个。被几个壮观场面(当然后面的算法要对)震撼了一遍,对牛顿力学的感知比中学大学五年加起来还要强烈。例二,tesla music. 我们这旮瘩有几个小年轻在车库里搭了两个tesla线圈,用音乐(大部分是游戏音乐)调制。我儿子看见就不肯挪窝。我老担心他的听力有没有受损,但是他对电的认识肯定要比我小时候深刻。更恰当的例子是您文中的几张图片。如果哪天画家能随心所欲的挥撒黎曼面和分型,数学教肯定已经一统江湖了.
M.Kline(就是写《古今数学思想》的那位)写过一本《西方文化中的数学》(Mathematics in Western Culture),我翻过一点,推荐老兄也看看,要是有新的感悟别忘了发原创若干。
比如里面有个例子,文艺复兴的绘画,大量使用透视,而与透视密切相关的数学叫做“射影几何”,也就借此东风红红火火发展起来。我以前帖子里提到的“椭圆几何”的简单模型,就是把球面的对径点粘合起来得到的,得到的那个东东叫做“射影平面”。
我一直有个小疑问。二十世纪文学艺术等领域兴起一股“结构主义”的风潮。而几乎在同时,数学也有“结构主义”。这两者并不能简单的等同起来,但它们的背后,从文化层面来看,有没有更深层次的联系呢?
回头去翻一下。恕我孤漏寡闻,数学上的结构主义是什么东西?
老兄告一段落后回头讲一下集合论(是只这个名目吗?)吧。
你想听什么?
基本上,今天学数学的把集合的语言作为最基本的语言,但也就仅此而已。要我讲出很多来还真不容易,哈哈。
我爱兄随意。
我有类似的体会,离开了这个我们体验的逻辑就无从谈起。有一个学哲学的朋友从一本书里找了些题来调戏我们,总之他假设的集合概念与我们体验的完全两样,纯逻辑游戏。老兄知道这本书的出处吗?
怎么猜呀。
哲学家里,像罗素,维特根斯坦等应该很懂集合论。我翻过维特根斯坦的《逻辑哲学论》,用公理体系把世界诠释了一遍,很好玩的。但只能说是对世界的一种理解吧。
集合论,以及公理体系等等,在100年前曾经风靡一时一代数学家试图把数学的基础,甚至物理的基础(比如希尔伯特)建立在它们上面。那个时代有过蛮多好玩的故事的,外头资料不少,一般叫做(由罗素悖论引起的)第三次数学革命。不过后来哥德尔定理的出现改变了不少人的观念。
今天的话,我自己的观念,包括认识的很多学数学的朋友,纯粹把集合论或者公理体系之类当作工具,或者说语言。数学,乃至自然科学的本源应该是更加深刻的东西。